Cette page peut être téléchargée en version Word ou PDF

4TPC1 EXERCICE (Thalès)

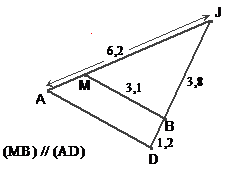
Répondre aux questions suivantes en donnant la valeur exacte puis la valeur approchée au dixième de l’unité.

1) Calculer AD.

2) Calculer MJ, puis MA.

4TPC2 EXERCICE (Thalès)

Une personne observe une éclipse de soleil.

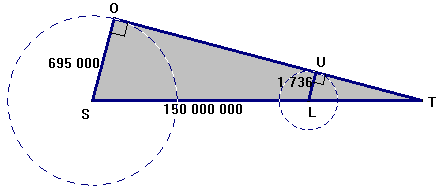
Cette situation est schématisée par le dessin ci-contre.

L’observateur est en T.

Les points S (centre du soleil), L

(centre de la lune) et T sont alignés.

Le rayon SO du soleil mesure 695 000 km.

Le rayon LU de la lune mesure 1736 km.

La distance TS est 150 millions de km.

Calculer la distance TL (On donnera l’arrondi au km).

4TPC3 EXERCICE (thalès- Pythagore)

Sur la figure ,les droites (VA) et (BC) sont parallèles.

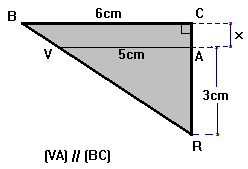
1) Calculer la longueur x .

2) Calculer la longueur VR

(On donnera l’arrondi au mm) .

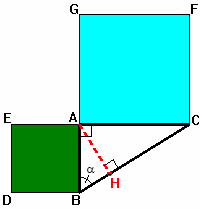
4TPC4 EXERCICE– Cosinus – (Inspiré par la démonstration d’Euclide du théorème de Pythagore)

Sur les côtés [AB] et [AC] d'un triangle ABC rectangle en A, on a construit les carrés ABDE et ACFG.

On a tracé aussi la hauteur [AH] du triangle ABC, issue de A.

On pose = a

1) a) Montrer que :

AB = et AB = BC cos a

b) En déduire que AB² = BH × BC

2) Donner une expression de AC²

à l’aide de CH et CB. ( A s’inspirer du résultat de 1 b) )

3) En déduire une expression de la somme AB²+ AC², à l’aide de BC.

4TPC5 EXERCICE (aire-pyth-cos)

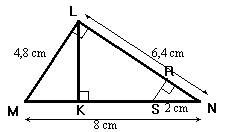
LMN est un triangle rectangle en L .

K est le pied de sa hauteur issue de L.

On donne :

MN= 8 cm ; ML = 4,8 cm ; LN = 6,4 cm.

( On ne demande pas de refaire la figure sur la copie.)

1) a)Montrer que l’aire du triangle LMN est égale à 15,36 cm².

b) Justifier que l’aire du triangle LMN est aussi égale à 4 KL

c) En déduire que KL = 3,84 cm

2) Montrer que : MK = 2,88cm.

3) Calculer et trouver : = 36,9° (valeur arrondie au dixième de degré)

4) Soit S le point de [MN] tel que NS = 2 cm.

La perpendiculaire à (LN) passant par S coupe [LN] en R.

Calculer RN (donner la valeur arrondie au millimètre prés).

4TPC6 EXERCICE (Pythagore)

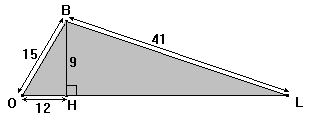
1) En utilisant les données indiquées sur la figure, calculer HL et OL.

2) Calculer l’aire du triangle BOL.

4TPC7 EXERCICE

On considère le triangle STR ci-contre.

H est le pied de sa hauteur issue de S.

1) Sachant que TH = 5 cm ; SH = 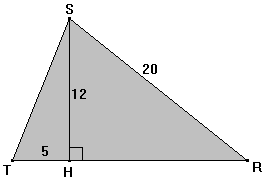12 cm et SR = 20 cm ,

calculer ST et HR .

2) Calculer alors l’aire du triangle STR.

4TPC8 EXERCICE (Extrait de Dimathème)-Th de Pythagore (contraposée et réciproque)

1) Le père LOUIS prétends que son champ, dont on a dessiné le plan ci –contre, les côtés [LI] et [IU] sont perpendiculaires.

A-t-il raison ?

2) Il dit aussi que les côtés [OU] et [OL] sont perpendiculaires.

Est-ce vrai ?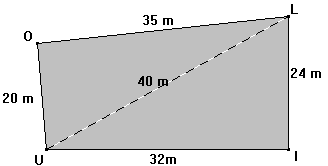

4TPC9 EXERCICE

Recopier et compléter :

5°

11°

. . . . . . .

37,6°

. . . . . . .

Cos

. . . . . . .

0,940

. . . . . . .

0,5

Donner : pour , la mesure arrondie au dixième de degré.

pour cos , la valeur décimale arrondie à 10^-3.

4TPC10 EXERCICE ( cosinus)

Soit ABC un triangle rectangle en A tel que :

= 62° et BC = 8cm

Calculer AB (arrondir au mm).

4TPC11 EXERCICE

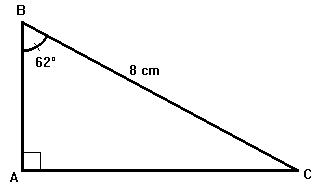
Calculer BC (arrondir au mm)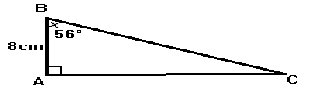

4TPC12 EXERCICE

Calculer ,

puis AB et AC arrondis au dixième.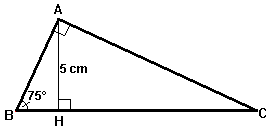

4TPC13 EXERCICE ( cosinus)

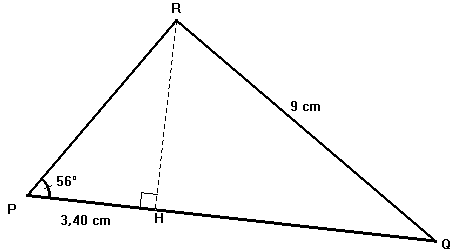
On considère la figure ci-contre représentant un triangle PQR rectangle en R et sa hauteur [RH] .

On donne :

= 56° ; PH = 3,40 cm et RQ = 9 cm.

1) Justifier que : = 34°

2) Calculer PR .

3) a) Calculer HQ .

b) En déduire PQ

4TPC14 EXERCICE

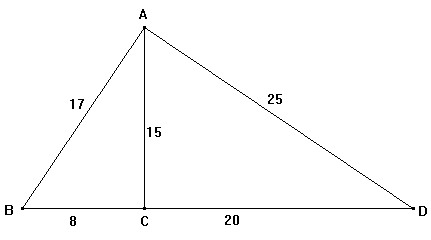Sur la figure :

AB = 17 m ; AC =15 m ; AD= 25 m. ;

BC = 8 m ; CD = 20 m

et les points B, C et D sont alignés

1) Le triangle ABC est-il un triangle rectangle ? - A justifier .

2) Le triangle ABD est-il un triangle rectangle ? - A justifier.

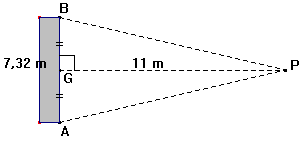
4TPC15 EXERCICE (Pythagore – Cosinus )

Un footballeur s’apprête à tirer un penalty.

Le ballon est posé sur le point P à 11m de la ligne de but.

Pour savoir sous quel angle le footballeur voit la cage

du gardien de but, fais le travail suivant :

1) Calculer AG.

2) Calculer AP ( arrondir au cm).

3) Calculer alors l’angle et en déduire